皆さん、こんにちは。草野球で極度のスランプに陥り、もはやトップのチームで結果を残せず、40歳以上のシニアチームで活動することを決断した検査課の白濱です。
体力は衰えても、脳ミソはそうなっては困るので、変わらず「趣味数学」を続けています。
今回のブログは、また、勝手に数学を解いたお話をします。(ブログネタがないのに書かないといけないからです。)
テキストは「大学入試の[抜け道]数学」という、当時、偏差値が伸び悩んでいた時の打開策用に買ったものです。
さて、問題は次の通りです。
例題85
実数、a,b,c に対して、3次の正方行列 A を次のように定義する。
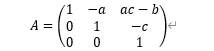
このとき、行列 A の逆行列 B を求めよ。
(香川医科大学)
まず、3×3の行列って高校数学の範囲外じゃね?もはや、反則な気がするけど、問題見た瞬間に方針が立ちます。
行列 B をなんちゃらって置いて AB=BA=E となるような B を求めろってことだよね。

と置いて
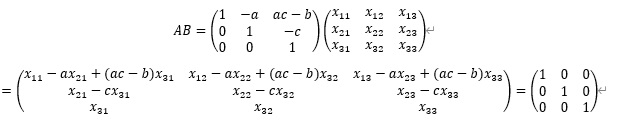
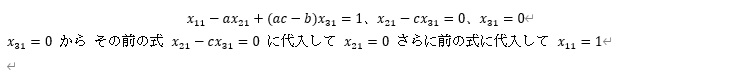
意外と計算面倒じゃないし、その後の計算を省略して
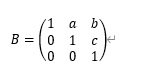
と解けましたがまだ終わりではありません。行列の積は×順番が違うと答えも違ってくるので BA を計算して単位行列 E になることを示さなければなりません。
もちろん、計算した結果、単位行列になったので、これが答えです。
さて、模範解答を見ると、「3×3行列の det と逆行列を求める公式は覚えておきましょう!」
公式より、答えは これ です。
はあ~?3×3行列のdet(行列式)の公式は確かにあった(名前は忘れた)けど、それって、大学の線形代数で出てきたし。逆行列の公式って、どんなんだっけ?
完全に反則技です。
慌てて、線形代数の教科書を調べると、余因子行列とか転置とか知ってないとだめだし、行列式の公式はあったけど、3次より大きい行列の行列式は?から定義を調べてみると、置換を理解していないとだし、、、、
いずれ、線形代数を勉強し直すつもりだったけど、こんなに難しかったか?
とりあえず、脳ミソが活性化されたので当初の目的は達成できました。
ちなみに、今の高校の教育課程では、行列は範囲外だそうです。
なんということでしょう!


