皆さんこんにちは。最近、自分の父親を見て、自分の将来の認知機能の低下を心配し始めた検査課の白濱です。
脳を活性化することなくボーっと生きていたところ、ふと「sinって微分するとcosだっけ」と公式を忘れている自分に気づきました。やばい、ボケの始まりか?
公式を忘れたなら、作ればいい。では、やってみよう。
ある点xで微分するとは、その点から少し幅を持たせて、そこの平均変化率を求め、その幅を小さくすればよい。さすがに、微分の定義は覚えているわ!
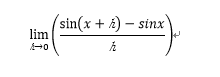
本当はプラスから近づく、マイナスから近づくとか調べて一致するとか連続性も確認しないとだけどここは省略。
さて、sin(x+h)だけど、確か展開する公式があったなあ。
やばい、これも覚えていない!
何とかならんか?sin(α+β)=sinαcosβ、、、んーどーだったっけ?「サイタコスモス、、、」とか覚え方あったような?おっ、良いこと思いだした。
単位円周上の点で、x軸からの角度がαの点をPとすると、その座標はP(cosα、sinα)。今、角(α+β)の点を問題にしているが、これは点Pをβ度回転させた点であり、その点をQとするとQ(cos(α+β)、sin(α+β))となる。
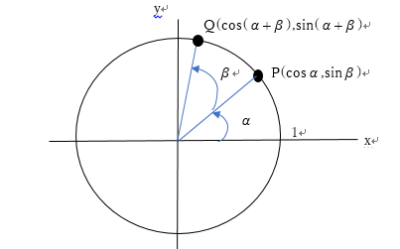
幸いにも、この一次変換を表す行列は覚えている!適用すると、
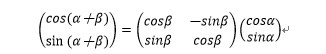
よしよし、sin(α+β)=sinαcosβ+cosβsinαと分かったぜ。
では、微分に戻ると
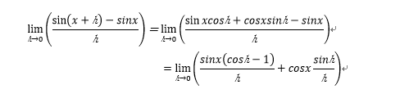
式変形のポイントは、sinxでくくることと、sinh/hの形を作ることかな?
h→0の時cosh→1で前項は0。h→0の時sinh/h→1だから、後項はcosx
因って、
![]()
でーきた!ふう、物凄く脳が活性化されたような気がする。


